
Para causar calafrios em alguns.
De certa forma, qualquer estudo da Natureza envolve o uso de "subterfúgios" para conseguir ser realizado. Como geralmente é impossível analisar todas as complexidades, nuances e sutilezas em torno de fenômeno, temos que desconsiderar tudo que possa ser irrelevante o até mesmo pouco significativo para as informações que queremos descobrir. O contexto - a reunião de todas as condicionantes de interesse de um fenômeno - é o que ditará o que deve ser cortado ou não. Assim, toda vez que for apresentado algo deste tipo:
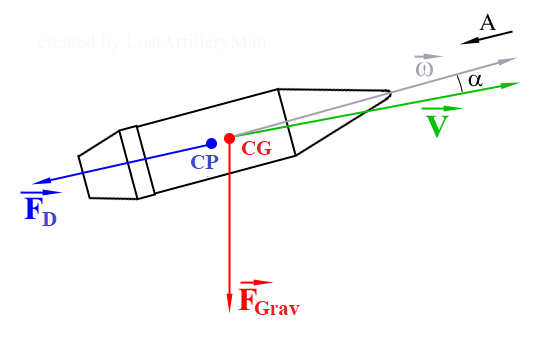
Lembre-se, isso não é um projetil, mas um modelo com o qual podemos trabalhar (1). Projetis reais estão disponíveis apenas durantes os exercícios de tiro ... ou na batalha!
Este capítulo visa apresentar o modelo em que o projetil sofre única e exclusivamente a atuação da força gravitacional nas proximidades do solo e distância menores que 10 km. Ou seja, consideraremos a aceleração da gravidade como uma constante, desprezamos a resistência do ar, e utilizaremos a aproximação da "Terra plana" para nosso proveito, a fim de utilizar apenas a matemática do Ensino Médio nas demonstrações.
Embora essas simplificações aparentem tornar o modelo projetil no vácuo inútil para aplicações práticas, há contextos reais em que pode dar boa precisão, como apresentaremos mais ao final. Além disso, por ter uma solução analítica simples, fornece vislumbres sobre o comportamento do voo que ficam muito imediatos em modelos mais sofisticados.
[índice]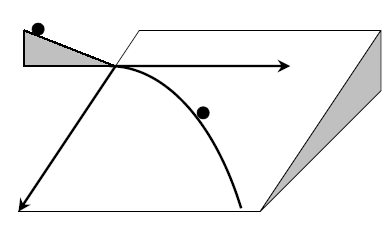
Fonte: [Nuffield Fundation]
Os primeiros estudos de como um movimento complexo poderia ser decomposto em movimentos mais simples e passíveis de análises independentes remontam a Galileu Galilei. A última parte de um de seus últimos trabalhos - o livro As Duas Novas Ciências, o "Quarto dia" -, é dedicada ao movimento dos projetis. Como ele não dispunha dos modernos radares Doppler, nem mesmo de cronômetros preciso, providenciou um forma de deixar o movimento "mais lento": fez rolar pequenas esferas untadas de tinta sobre um plano inclinado, após serem elas impulsionadas a partir de uma lateral.
Ilustrações tiradas de As Duas Novas Ciências, o "Quarto dia".
Resgatando o tratado do grego Apolônio sobre seções cônicas, Galileu avaliou a proporção (bd/fe)2=ad/ae para a parábola, que era o padrão esperado pela composição de movimentos (e de experimentações, também). Embora ele, de forma um tanto confusa, utilizasse os segmentos horizontais tanto para se referir ao tempo como à distância lateralmente, essa confusão não invalida o resultado, pelo fato de haver proporcionalidade entre o tempo e a distância horizontal percorrida, em razão da constância da velocidade nessa direção. Assim, enunciou seu teorema:
Um projetil que é levado por um movimento horizontal uniforme, em composição com um movimento vertical naturalmente acelerado, descreve um caminho que é uma semiparábola.
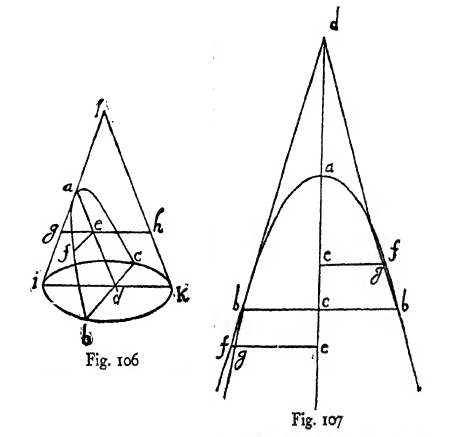
De fato, Galileu não estudou nesse livro o lançamento oblíquo. Um tratamento mais completo da trajetória de um projetil no vácuo foi dado por Newton no começo do segundo tomo de Principia, décima proposição, como uma prévia do estudo de projetis em meio resistivo. E também foram usados métodos geométricos.

Extrato de Principia Mathematica, com a dedução da trajetória parabólica para um projetil no vácuo. Edição em língua inglesa de 1846.
O tempo passou, e as ferramentas à disposição dos físicos cresceram e melhoraram. A fusão ocorrida entre a álgebra e a geometria há de nos ajudar.
[índice]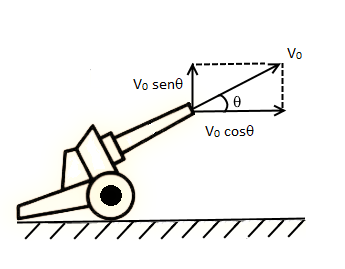
Componentes da velocidade inicial.
Um projetil lançado com uma velocidade inicial V0, a um ângulo θ em relação à horizontal do solo, terá como velocidades iniciais nas direções vertical e horizontal as projeções ortogonais de V0. No caso, V0 sen θ e V0cos θ, respectivamente, conforme a ilustração acima. Visto não estar sob ação de nenhuma força, a componente horizontal se mantém inalterada durante toda a trajetória, do lançamento ao impacto. Assim a velocidade horizontal é representada, em razão do tempo t, por uma função constante Vx(t) = V0cos θ.
Gráfico da velocidade horizontal em função do tempo para uma velocidade inicial de 100 m/s e elevação de 60º.
Considerando-se a peça sobre a origem do sistema de referência posicional, a cada intervalo regular de tempo, a distância para a origem da trajetória que uma hipotética "sombra" do projetil, perpendicularmente lançada sobre solo (2), aumentaria regularmente, em proporção ao tempo. Dessa forma, o retângulo sob o gráfico de velocidade horizontal até o instante t totaliza a distância percorrida nessa direção desde a origem.
Gráfico sombreado da velocidade horizontal em função do tempo para uma velocidade inicial de 100 m/s e elevação de 60º, indicando o total percorrido ao longo da direção horizontal.
Assim, por geometria simples, a posição horizontal X do projetil em função do tempo, a partir da origem, é dada por X(t) = tV0cos θ, i.e., uma função linear a partir da origem, cuja tangente do ângulo de inclinação é a velocidade horizontal.
Gráfico da posição horizontal em função do tempo para uma velocidade inicial de 100 m/s e elevação de 60º.
Como "tudo que sobe tem que descer", temos de lidar com velocidade variável na direção vertical. Podemos, inicialmente, começar a investigar de o movimento nessa direção de forma análoga a que fizemos para a horizontal, porém começando com a aceleração gravitacional, que pressupomos ser a constante nessa direção com o valor de g = -9,8065 m/s2. O sinal negativo para ela se dá em razão de havermos arbitrado o sentido "para cima" como sendo positivo. Ou seja, ao sair do tubo da peça, o projetil passa a ser "freado" pela força gravitacional.
Gráfico da aceleração gravitacional vertical, em função do tempo.
Neste caso, a "área sob o gráfico" se encontra abaixo do eixo das abscissas, significando uma taxa constante de perda de velocidade ao longo do tempo de valor -gt. Salvo o encontro do projetil com algum anteparo, em certo instante o sentido do movimento vertical se inverte e o módulo da velocidade vertical torna a crescer, agora em queda.
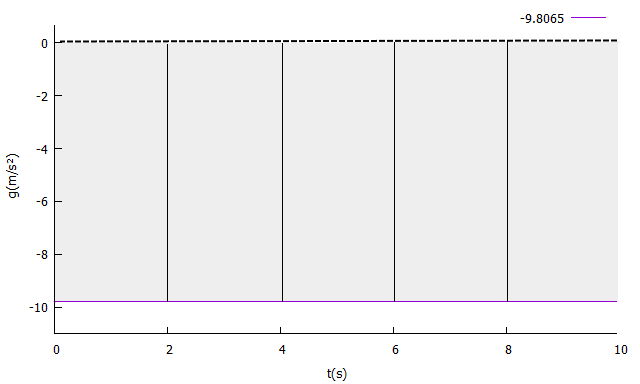
Gráfico sombreado aceleração gravitacional em função do tempo, cuja área representa o efeito cumulativo da força gravitacional.
Como a velocidade vertical inicial é V0sen θ, velocidade vertical é representada, em função do tempo t, por Vy(t) = V0sen θ - gt. Seu gráfico, portanto, é o de uma função linear decrescente, a cortar o eixo das ordenadas no valor da velocidade vertical de lançamento, e cuja tangente da inclinação é o valor da gravidade.
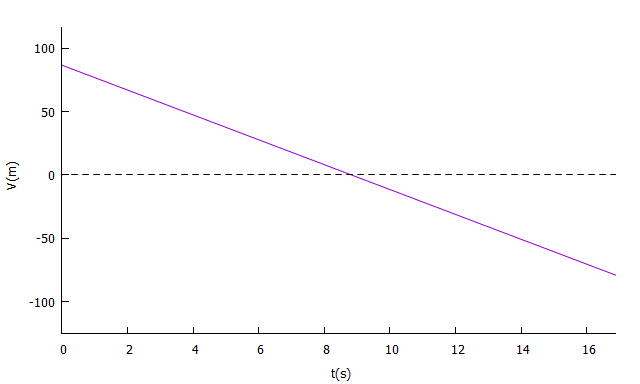
Gráfico da velocidade vertical vertical em função do tempo, para uma velocidade inicial de 100 m/s e elevação de 60º.
Neste caso, o instante de inflexão em que a reta corta o eixo das abscissas [tinfl = (V0sen θ)/g] representa o instante de inversão do movimento.
Agora que estamos lidando com velocidade variável, torna-se menos direta a determinação do quanto o projetil percorreu durante sua subida e, sendo o caso, sua descida também. O que não nos impede, contudo, de usar um estratagema para resolver essa questão. Imagine que um projetil "alternativo" mantivesse sua velocidade vertical de lançamento inalterada por quatro segundos. Findo esse tempo, sua velocidade seria instantaneamente "atualizada" com o valor que teria caso fosse um modelo "real" (uma amostra), mantendo-a pelos próximos quatro segundos, e assim por diante. Poderíamos, então, calcular a distância percorrida dentro desses fictícios "intervalos de velocidade constante" pela área de retângulo e somá-las para obter o saldo final, como na figura a seguir:
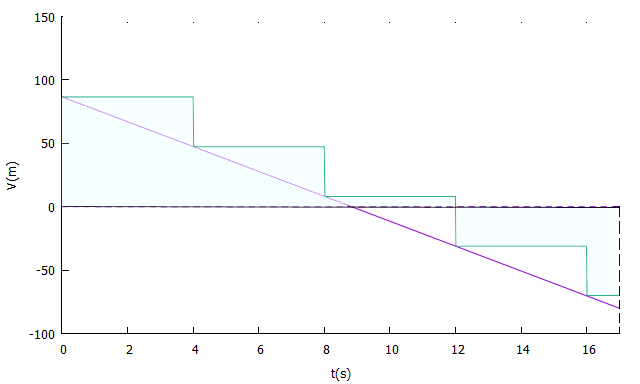
Gráfico sombreado da velocidade vertical em função do tempo para uma velocidade inicial de 100 m/s e elevação de 60º, estimando o total percorrido ao longo da direção vertical por amostragens a cada quatro segundos.
Constata-se, por rápida inspeção visual, grande discrepância entre o sombreado entre os lados esquerdo/direito do gráfico, sugerindo uma aproximação grosseira. Façamos, pois, amostras a cada dois segundos:
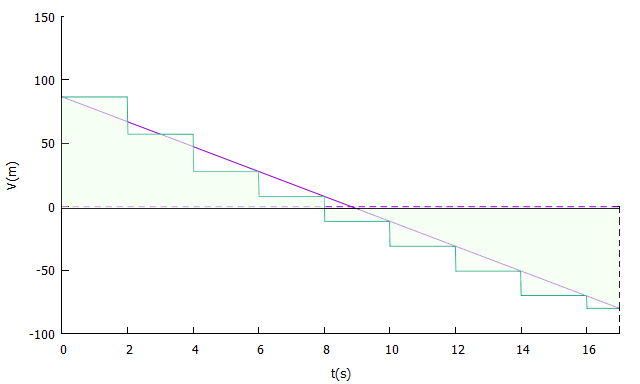
Idem, com amostragens a cada dois segundos.
Parece sugestivo, vamos amostrar a cada segundo:
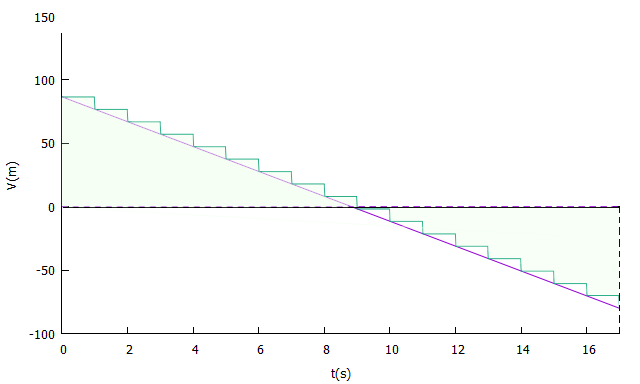
Idem, com uma amostragem por segundo.
Assim, a medida que são reduzidos os intervalos de "velocidade constante" e, na mesma proporção, acrescida a quantidade de amostras, o somatório das fatias retangulares se aproxima dos triângulos acima e abaixo da reta, conforme a velocidade vertical seja positiva (ramo ascendente da trajetória) ou negativa (ramo descendente). Assim, para determinarmos o quanto a posição vertical do variou, basta determinar o "saldo" entre as áreas positiva e negativa dos triângulo. Isso leva a dois casos:
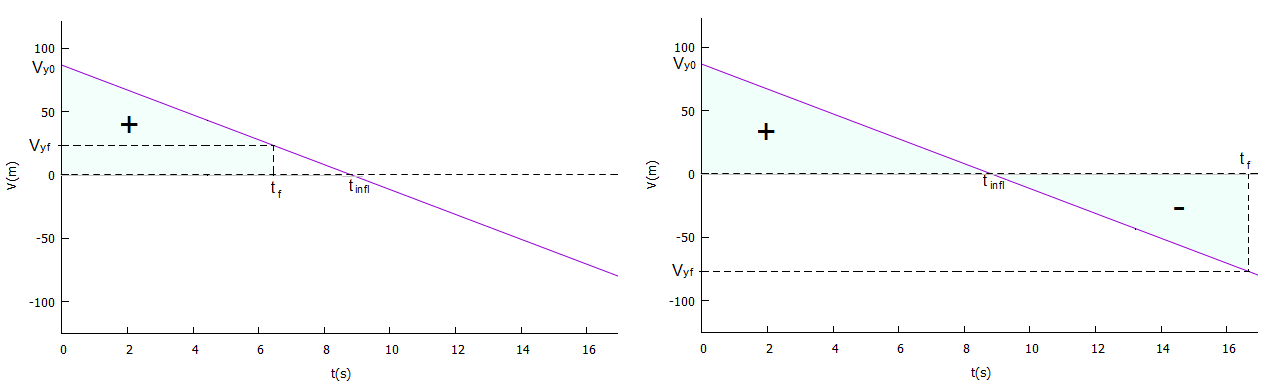
Duas situações possíveis quanto a área sob o gráfico da velocidade vertical.
Assim, a distância percorrida será:
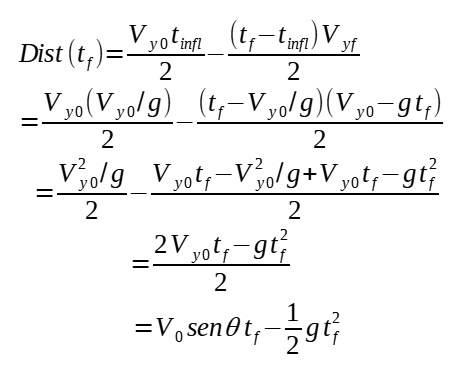
Fazendo tf ≡ t e considerando como de altura zero a posição y(0) da peça, então;
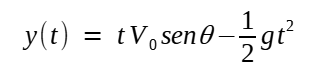
Sumarizando, as fórmulas para o lançamento oblíquo de um projetil no vácuo são:
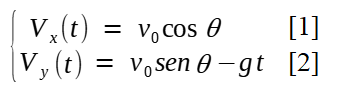
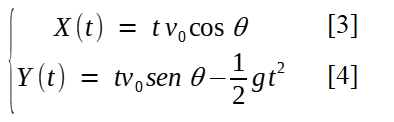
Que também são conhecidas como equações horárias do movimento do projetil no vácuo ou equações paramétricas (sendo o tempo t o parâmetro). Elas serão o ponto de partida para a determinação das propriedades desse modelo de projetil.
[índice]
Parábolas da Natureza (fonte: WikiMedia Commons).
Tendo como base as equações horárias deduzidas na seção anterior, serão demonstradas algumas propriedades matemáticas do voo no vácuo.
Tomando-se a equação horária [3 e exprimindo o tempo t em função da posição horizontal x:
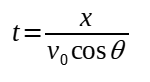
Substituindo em [4]:
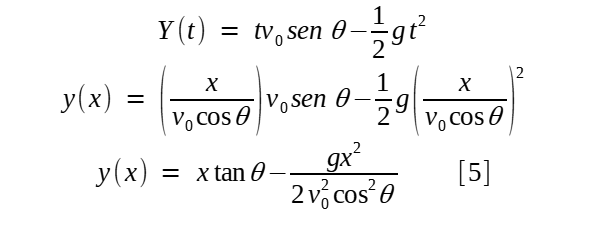
Que é uma função quadrática, cujo gráfico é uma parábola com a concavidade para baixo, pois seu coeficiente em x2 é negativo. Repare, também, que ela será a mesma para qualquer projetil disparado de um ângulo θ, pois sua massa e forma só se tornam relevantes ao se considerar a restistência do ar.
Baseando-se nas propriedades dessa figura geométrica, avaliaremos outras características da trajetória no vácuo.
Supondo que o ponto de disparo e o de impacto estejam na mesma altitude, então eles serão as raízes da equação de segundo grau [5], deduzida acima. Assim, pela simetria da parábola, o vértice da trajetória estará a meio caminho desses pontos. Poderíamos obter as coordenadas (xV; yV) do vértice da parábola a partir de fórmulas da geometria analítica, mas faremos uma abordagem um pouco diferente.
O vértice da trajetória se dá, no domínio do tempo, quando o sentido da velocidade vertical está na iminência de se inverter, i.e., quando Vy(t) = 0. Já calculamos anteriormente que isso ocorre quando t = (V0sen θ)/g e, aplicando esse valor na equação horária da posição [3], temos:
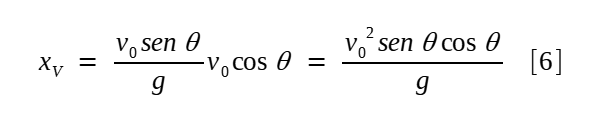
Da mesma forma, a partir de [4]:
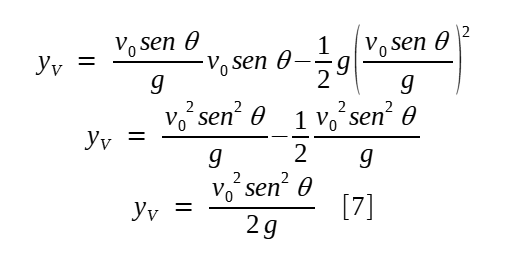
Como uma parábola é simétrica em relação ao eixo vertical passando pelo vértice, o alcance coplanar é o dobro daquele para o vértice.
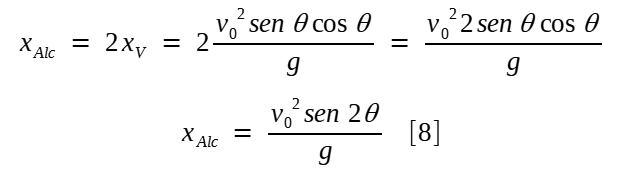
A fórmula acima fornece a magnitude máxima quando sen 2θ for igual à unidade. Delimitando-se θ entre 0 e 90o, então:
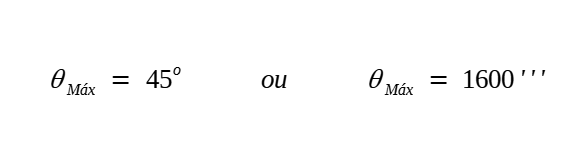
De forma análoga, o tempo de voo até o impacto será o dobro do tempo de inversão do sentido da velocidade vertical.
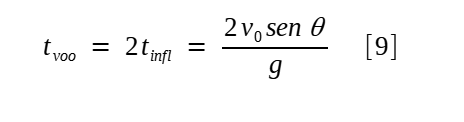
A maior pergunta de um atirador não é saber onde incidirá o tiro que ele realizou em determinada posição, sob determinado ângulo, mas o que chamamos de problema reverso: "como ajustar a angulação de meu armamento de modo a fazer meu tiro incidir onde preciso?" Com a equação [8], sabemos o alcance para um ângulo de disparo θ. A partir dela, façamos o inverso: obter o ângulo necessário para se bater determinado alcance:

Dado que -1 ≥ sen θ ≤ 1 e, na prática, θ ≥ 0; então é necessário que (gxAlc)/(v02) ≤ 1 para seja possível bater o alvo com algum ângulo θ. Do contrário, será preciso reduzir o alcance almejado ou aumentar a velocidade inicial.
Outra propriedade apresentada por [10] é a possibilidade de se bater um mesmo alcance por dois ângulos distintos. Embora a função arco seno tenha seu domínio em [-π/2; π/2], também sabemos que sen(x) = sen(π - x) , i.e., ângulos suplementares têm o mesmo seno. Como há o fator 1/2 em [10], então ângulos complementares batem o mesmo alcance.
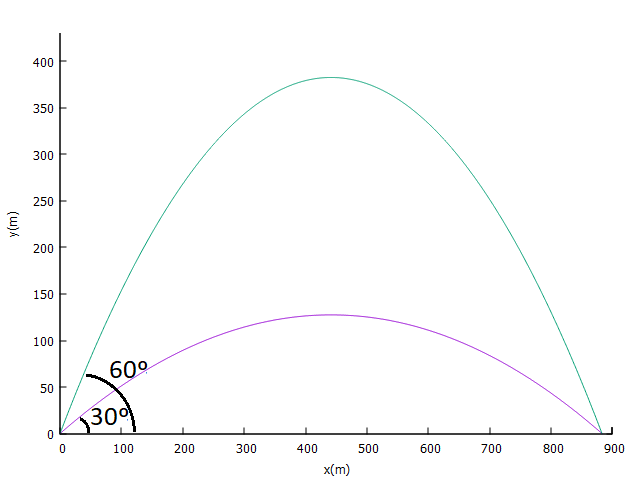
Trajetórias no vácuo para projetil de V0 = 100 m/s, θ1 = 30o e θ2 = 60o.
A tangente do ângulo terminal (ou de queda) é dada pela razão entre a velocidade vertical e a horizontal no instante do impacto, visto serem elas as componentes da velocidade tangencial. Sabemos que a componente horizontal se mantém constante, com o módulo de V0 cos θ. Para obter a velocidade vertical, aplicamos o tempo de voo [9] obtido acima na equação horária da velocidade vertical:
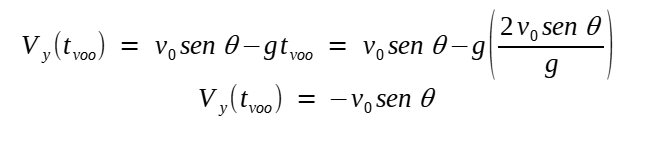
Assim, o ângulo terminal terá como tangente tg θf = (-V0 cos θ)/(V0 cos θ) = - tg θ = tg(π - θ). Isto é, o ângulo terminal, do ponto de vista do sistema de eixos, é o suplemento do ângulo de disparo, ou idêntico a ele caso medido da parte interna da trajetória.
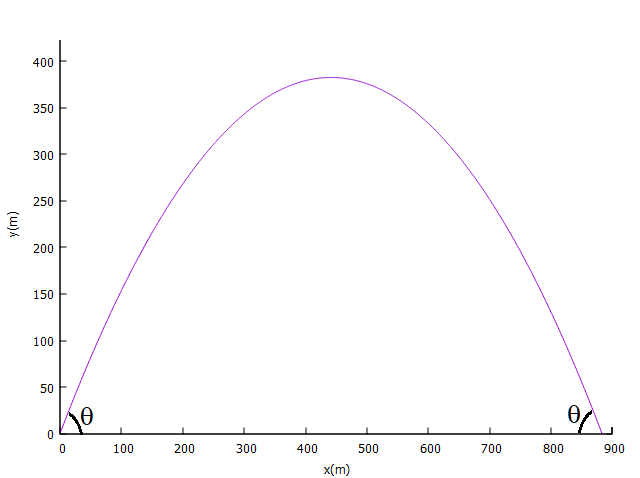
Trajetória no vácuo para projetil de V0 = 100 m/s e θ = 60o.
A ordenada máxima é a correspondente ao vértice da trajetória. Utilizando-se a equação horária da posição vertical [4] e aplicando-lhe o tempo de inflexão tinfl, temos:
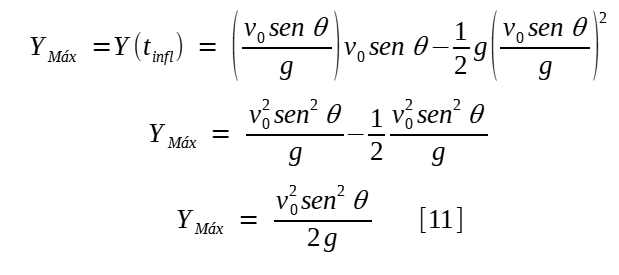
Agora, faremos algumas manipulações algébricas para expressar a ordenada máxima por meio de outro parâmetro:
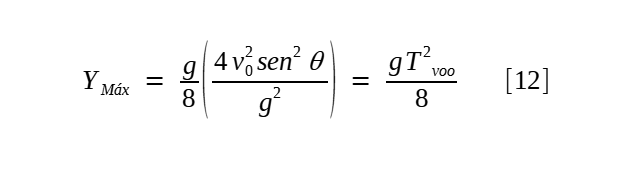
Tal relação será será útil para explanar uma propriedade das tabelas de tiro, como vermos mais adiante.
[índice]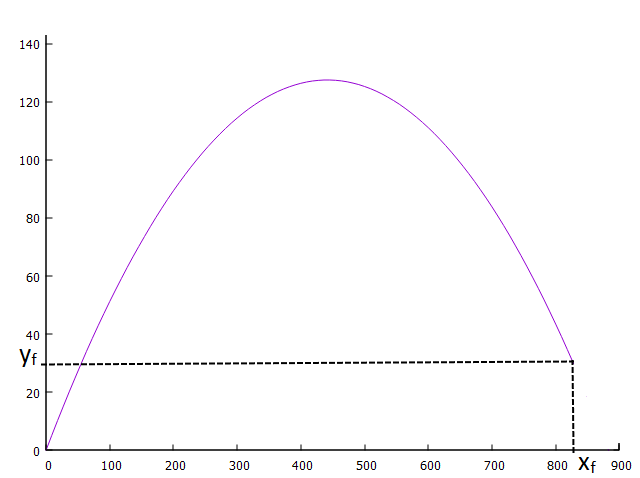
Trajetória no vácuo com desnível (xf; yf) para projetil de V0 = 100 m/s e θ = 30o.
Até o momento, trabalhamos com o pressuposto de que os pontos de disparo e impacto se encontram sobre o mesmo nível do solo, algo pouco comum no mundo real. Para todas as demais situações:
Ainda falta a obtenção do ângulo de disparo necessário, que demandará um pouco mais de trabalho. Tomando a equação da trajetória [5], aplicando-lhe o ponto desejado (xf; yf), e lembrando que 1/cos2 θ = sec2 θ :
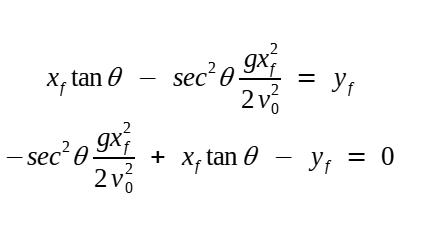
Aplicando a identidade sec2 θ = 1 + tan2 θ
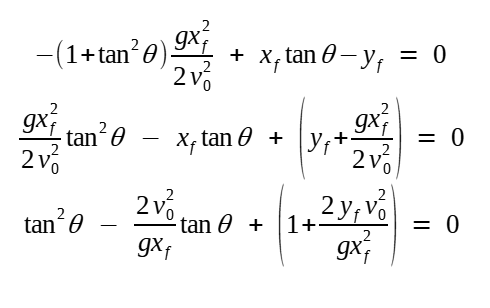
Agora, valhamo-nos da equivalência u ≡ tan θ :
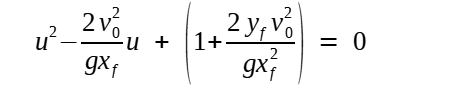
Que é uma equação do segundo grau na variáviel auxiliar u. Aplicando a boa e velha fórmula de Bhaskara:
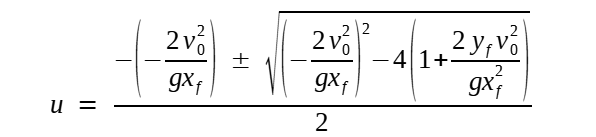
Após alguma manipulação algébrica, temos:
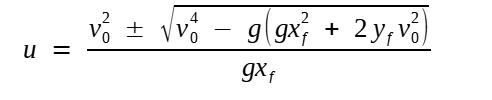
Enfim:
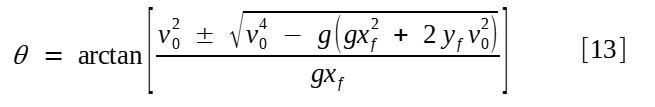
Caso o radicando seja positivo, haverá duas soluções, i.e., dois possíveis ângulos para os quais é possível acertar o alvo na coordenada (xf; yf). Caso negativo, então a velocidade inicial v0 é insuficiente para bater o alvo, sendo necessário aumentar a carga do propelente.
Agora suponhamos um ponto (xf; yf) esteja ao alcance de um armamento a uma dada velocidade inicial v0. Quando yf for positivo, um incremento no módulo desse desnível (i.e., o alvo "sobe" no horizonte) reduzirá o valor do radicando até que ele se torne negativo, e não seja mais possível atingir o alvo. Por outro lado, para um yf negativo, a medida que o alvo "descer" no horizonte, o valor do radicando aumentará, sendo sempre possível atingir o alvo para o xf considerado. Em outras palavras, neste modelo há um limite para o sítio positivo, mas não para o negativo.
[índice]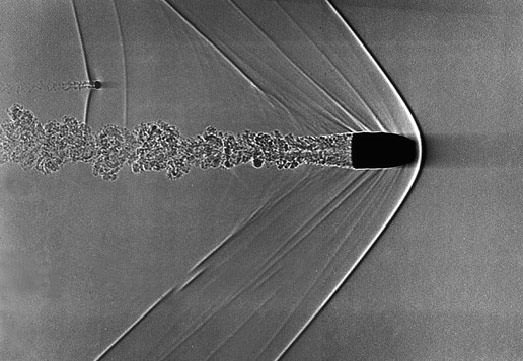
Projetil disparado a velocidade supersônica. Repare na frente de onda à sua dianteira e nas turbulências que se formam atrás.
(Créditos: Andrew Davidhazy/Rochester Institute of Technolog).
É quase um truísmo descartar o uso do modelo da trajetória no vácuo para aplicações práticas em razão de ele desconsiderar a resistência do ar. Entretanto, daí vem a pergunta: haveria situações em que ela teria uma magnitude pouco importante quando comparada à da gravidade? Bem, a influência de resistência do ar pode ser entendida como o resultado das colisões das moléculas de seus gases sobre a superfície do projetil, que é moldado pelos seguintes fatores:
Existe um número conhecido Coeficiente Balístico (CB) que pode ser entendido como a capacidade de um corpo superar a resistência do ar durante voo (3). Uma de suas formulações matemáticas é:
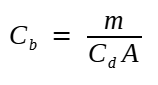
Em que m é a massa do corpo, A a área da seção reta na direção do deslocamento, e Cd um número adimensional chamado "Coeficiente de Arrasto" (Drag Coefficient, em inglês), cujo valor depende tanto do perfil aerodinâmico do corpo quanto de sua velocidade (4). Retornaremos a ele quando falarmos em modelos realistas de resistência do ar. Em projetis, a seção reta é um círculo cujo diâmetro é o seu calibre; Cd é pequeno em velocidades subsônica, tendo um pico nas proximidades da barreira do som, para, em seguida, decair lentamente.
Seguem, então, dois exemplos com coeficientes balísticos diferentes, ambos com disparos a 265''' (~15º) em que são confrontados o modelo de trajetória no vácuo e um com a resistência do ar proporcional ao quadrado da velocidade (5):
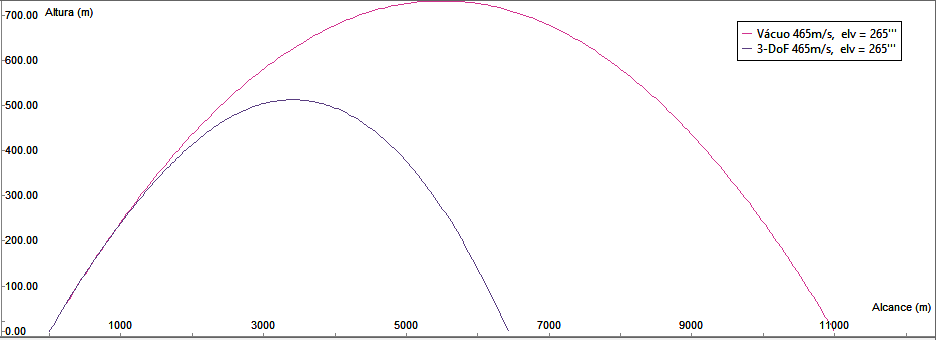
Disparos com e sem resistência do ar para o projetil 105 mm HE, a 465 m/s.
Para um projetil de calibre 105 mm (14,96 kg), a velocidade inicial testada foi a da mais alta carga (Cg 7) da tabela 105-H-7 (ca. 465 m/s), caindo para cerca de 287 m/s no impacto (queda de 38,3%). O Cb inicial (6) é de 4.438,4 kg/m2. Por simples inspeção no gráfico, o leitor pode constatar um erro de aproximadamente 3.500 metros a mais no alcance, o que torna proibitivo o uso o modelo de trajetória no vácuo nestas circunstâncias.
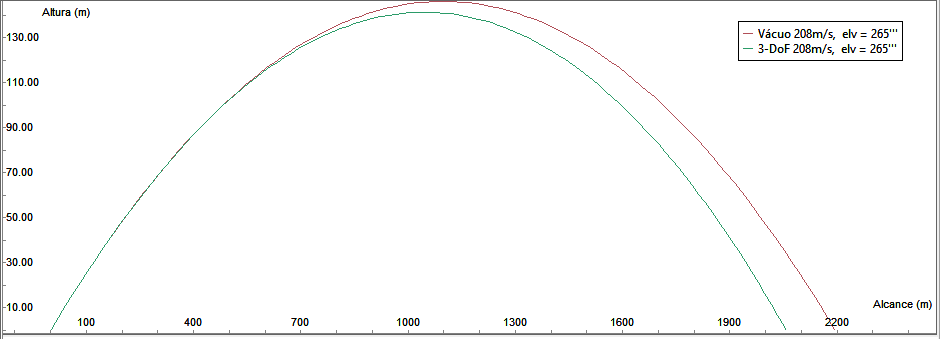
Disparos com e sem resistência do ar para o projetil 155 mm HE, a 208 m/s.
Neste exemplo, temos um projetil de calibre 155 mm (43,09 kg) disparado à velocidade da menor carga da tabela 155-AM-2 (Cg 1G), terminando a trajetória em cerca de 190 m/s (queda de 8,7%). O Cb inicial (7) subiu para 16.054,2 kg/m2. Agora o erro foi de menos de 150 metros a mais no alcance, compatível com o que se esperaria de uma peça não regulada. Assim, seria viável, na absoluta falta de qualquer outro recurso, o emprego do modelo de trajetória no vácuo para projetis pesados (155 mm de calibre ou mais), a velocidades bem abaixo da barreira do som, e alcances curtos.
[índice] - Curva Envoltória
- Curva Envoltória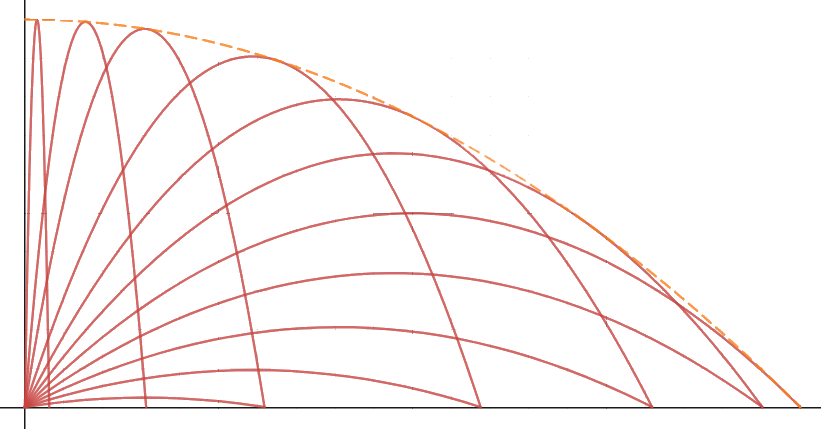
O manual C6-40, no primeiro capítulo do primeiro tomo (seção 1-14) diz:
O conjunto dessas trajetórias é envolvido por uma curva que é tangente a cada uma delas. Essa curva, que tem o nome de curva de segurança, limita, no plano de tiro, a região dos pontos que podem ser atingidos pelo material em apreço, atirando a mesma munição com a velocidade inicial considerada. Pontos tais como M1 e M2, situados no interior da curva de segurança e abaixo da trajetória de alcance máximo, podem ser atingidos por duas trajetórias.
Qual é o tipo geométrico dessa curva de segurança, isso não é informado. Até porque, para os modelos mais realistas de trajetórias, não é uma das figuras tradicionalmente vistas nos bancos escolares. Por outro lado, para a trajetória no vácuo, a curva se mostra ser a bem conhecida parábola:
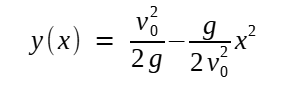
Por não possuir um termo linear em x seu vértice se encontra em x = 0, cuja ordenada é altura que o projetil atinge quando disparado verticalmente (y = v20/(2g)). Seu "zero positivo" (x = v20/g) corresponde ao alcance máximo, quando θ = 45º. A dedução dessa parábola é um tanto complicada e foi deixada para a nota de número (8).
[índice] - Tabela C
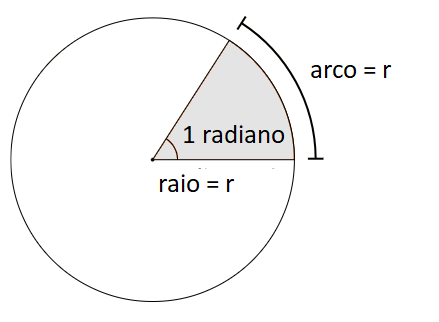
- Tabela CJá que estamos falando em composição de movimentos, vejamos a tabela C do STANAG 4119, que trata da decomposição das componentes do vento. Antes, porém, façamos uma rápida incursão sobre medidas angulares, e como elas se desenvolveram até o seu emprego na Artilharia.
Basicamente, as mais comumente unidades de medidas de ângulos são:
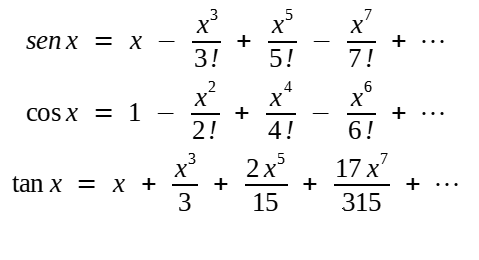
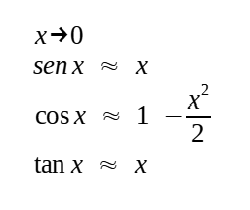
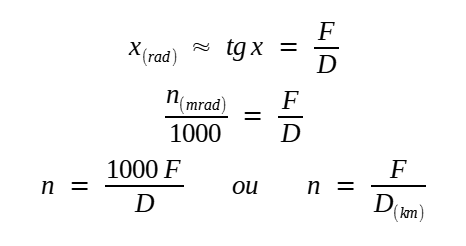
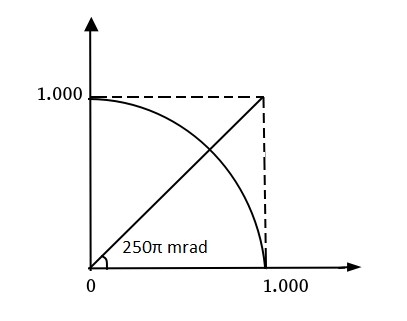
Após essa breve apresentação - um tanto histórica - dos sistemas de medidas angulares, vejamos como são aplicados em sistemas de coordenadas. Duas características se sobressaem:
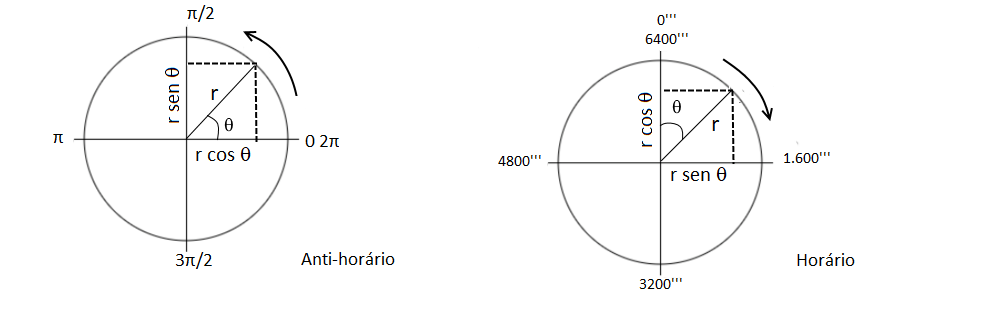
Em matemática, é o utilizado o sentido anti-horário, tendo como partida o semieixo horizontal positivo, além da métrica em radianos. O valor do seno de um ângulo θ é definido como a projeção de um raio unitário - da origem à posição do ângulo sobre a circunferência - sobre o eixo vertical. Analogamente, o cosseno corresponde à projeção horizontal. Em cartas militares, a relação com o plano cartesiano é um pouco diferente: os ângulos são medidos a partir do semieixo positivo vertical (em consonância com a direção do norte) e no sentido horário. Com isso, o que é seno se torna cosseno e vice-versa.
Após toda essa preparação, chegamos à Tabela C do STANAG 4119: Componentes para o um vento de um nó. Segundo a explanação de seu anexo I:
As componentes de um vento de um nó [0,51 m/s]. Um vento de um nó, soprando a partir da inclinação do vento sobre o plano de tiro (14), dividido em duas componentes; o vento transversal, perpendicular ao plano de tiro, e o vento de alcance, paralelo ao plano de tiro. Estes componentes devem ser multiplicados pela velocidade do vento da linha apropriada da mensagem meteorológica para obter o vento total transversal e de alcance a ser utilizado no problema específico do tiro.
Uma das formas de se construir essa tabela - e uma das mais comumente usadas nos materiais atualmente em uso no Brasil - é esta:
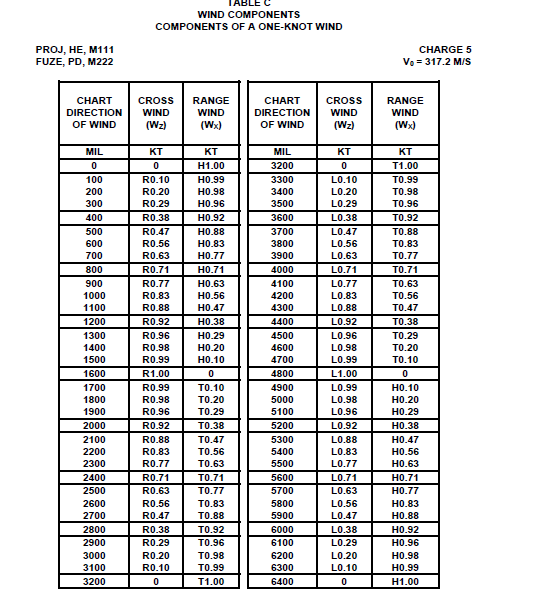
Em conformidade com os valores com as correções unitárias das colunas da tabela F do STANAG 4119, em vez de "positivo" ou "negativo" as componentes estão ajustadas conforme da direção de onde sopra o vento, i.e., de onde "ele vem". Assim R para o vento lateral vindo da direta (Right, em inglês) e L para o vindo da esquerda (Left), ao passo que temos H para o vento longitudinal contrário (Head, "cabeça" em inglês) e T para o a favor (Tail, "cauda" em inglês). Escolhendo o ângulo de 2200''', temos seu valor em radianos como θ ≈ 2,16 rad. Pode-se constatar que sen θ ≈ 0,8314 e cos θ ≈ -0,5557. Portanto, a tabela C é uma tabela de seno e cosseno (15) adaptada às correções de tiro para o vento, estando essas posições trocadas em relação ao que seria no círculo trigonométrico convencional .
Como essa tabela depende apenas do ângulo de inclinação do vento sobre o plano de tiro, ela será idêntica para todos os materiais adotados, independentemente da carga usada no exercício de tiro.
[índice] - Estimando a Ordenada Máxima
- Estimando a Ordenada MáximaÉ possível que o leitor já tenha travado contato com a formula Ymáx = (5/4) t2 para o cálculo da ordenada máxima, em que t é o tempo de voo. Ela é uma aproximação, mais fácil de memorizar, para a fórmula [12] deduzida acima:
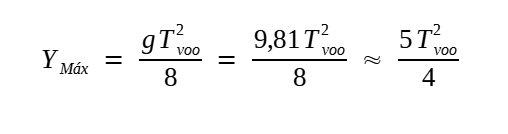
Atentemos que essa fórmula foi deduzida apenas para a trajetória no vácuo. Entretanto, empiricamente ficou constatado que ela fornece uma boa aproximação para trajetórias sob o efeito da resistência do ar (16).
| Tabela | Carga | Trajetória | Alcance (m) | Tvoo (seg.) | OM tabelada | OM estimada |
|---|---|---|---|---|---|---|
| Obus 105mm M101 H7 | 7 | Merg | 10.000 | 37,4 | 1.773 | 1.715,2 |
| Obus 155mm M114 Q4 | 5W | Vert | 8.000 | 59,7 | 4.340 | 4.370,5 |
| Mrt 120 mm Pr | 9 | Vert | 6.000 | 51,7 | 3.224 | 3.277,6 |
| Obus 155mm AR-1 | 7W | Merg | 14.000 | 50.8 | 3.273 | 3.164,5 |
Obs: ordenada máxima estimada usando-se g = 9,81 m/s.
[índice]Não rejeite a trajetória no vácuo prontamente e não a aceite cegamente, também. Identifique os vislumbres que ela pode oferecer.
[índice]
"Isto não é um cachimbo" (1929). Este quadro do pintor surrealista belga René Magritte nos dá uma boa intuição da diferença entre a realidade e sua representação.
(2) Caso fosse projetada pelo Sol, tal condição só seria satisfeita ao meio-dia, sobre a linha do Equador, por ocasião de um dos equinócios. voltar
(3) Em [Litz (2015)], cap. II, p. 33, aparece uma informal definição de coeficiente balístico como "a medida do quão bem uma bala penetra o ar". Sua fórmula também é um pouco diferente (adaptada para o Sistema Internacional de unidades):
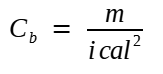
Em que m é a massa, cal o calibre, e i é um fator de forma adimensional. A proposta dessa outra formulação é permitir uma melhor comparação entre projetis, em especial os destinados a armas leves. Como todos possuem a seção reta circular, a constante π é desconsiderada; i é calculado, grosso modo, como a razão entre os valores da curva do coeficiente de arrasto Cd de determinado projetil com os da curva de outro tomado como padrão, de modo que a última (parcialmente) se sobreponha a primeira, caso sua função seja multiplicada por i.
(4) Seguem os gráficos de Cd para dois padrões de projetis: G1 e G7
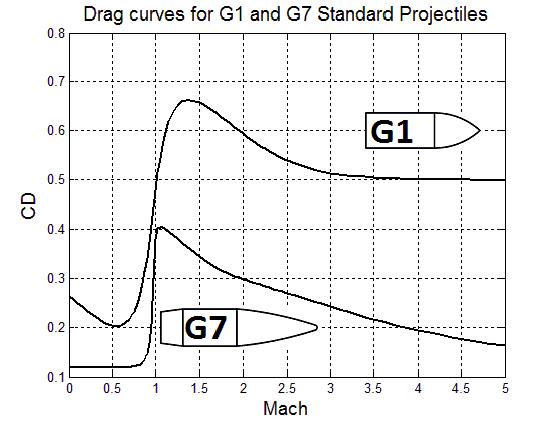
Fonte: [Litz (2021)]
O valor de um mach corresponde à velocidade do som no ar, em nível do mar e temperatura de 15 ºC (cerca de 343 m/s).
(5) No caso, foi usado o modelo de Três Graus de liberdade ou 3-DoF (Three Degrees of Freedom, em inglês). Os "graus" são as três direções de translação possíveis, e o corpo é considerado como pontual.
(6) Para o cálculo, foi considerado Cd = 0,39 para essa velocidade. voltar
(7) Para o cálculo, foi considerado Cd = 0,1428 para essa velocidade. voltar
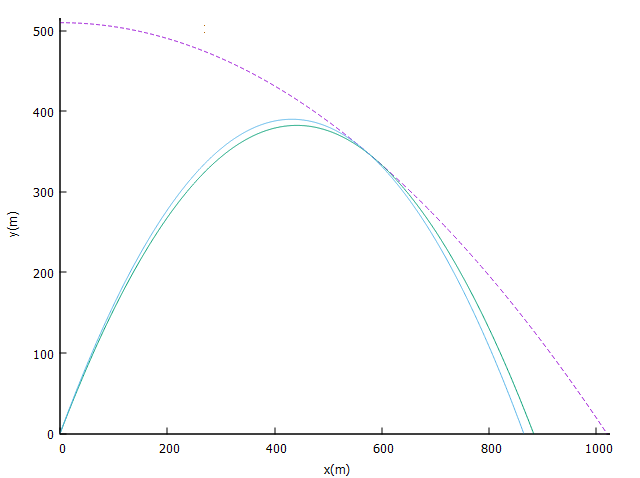
Envoltória para v0 = 100 m/s e trajetórias disparadas a θ = 60º e θ +ε = 61º.
Considere duas trajetórias com a mesma velocidade inicial e ângulos de disparo ligeiramente diferentes θ e θ + ε, cujas trajetórias são definidas por:
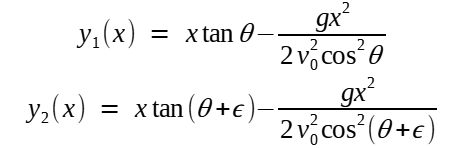
A envoltória passa pela intersecção dessas duas trajetórias ligeiramente diferentes, ou seja, quando y1(x) = y2(x):
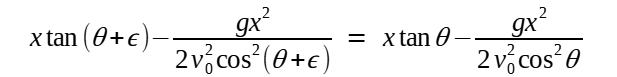
Desconsiderando a solução trivial (x = 0), então:
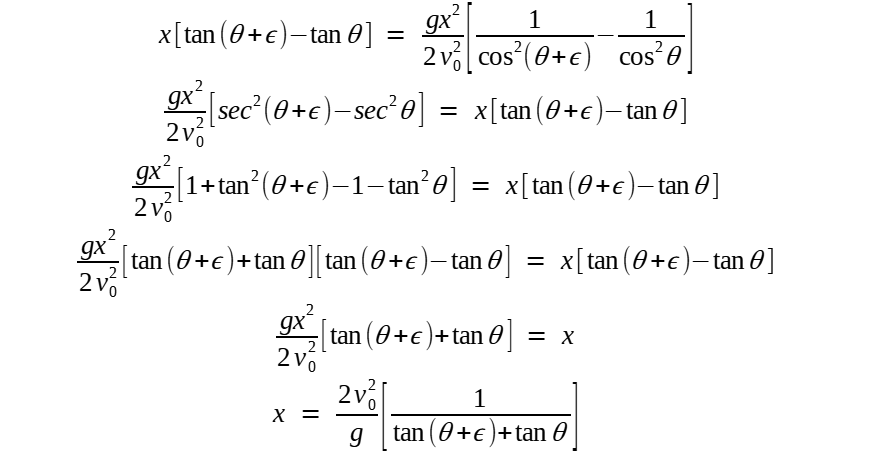
Agora, realizando a passagem ε → 0.
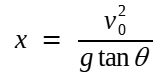
Substituindo este valor na equação da trajetória, a fim de também relacionar y com θ:
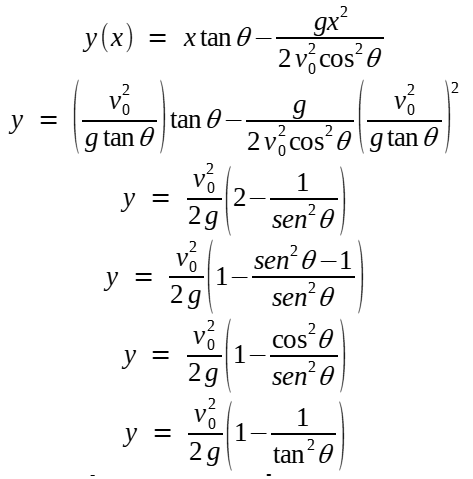
Por fim, um pequeno "passe de mágica" consiste em reescrever y de modo aflorar a expressão de x em função de θ:

Esta demonstração se calcou em manipulações com a quantidade infinitesimal ε, ou seja, um termo arbitrariamente pequeno que é usado para prevenir indefinições (como uma divisão por zero), até ser descartado quando não mais necessário. Os matemáticos não consideram essa prática como algo logicamente sólido, embora ela tenha mais trânsito entre os físicos. Há outras demonstrações mais rigorosas (cf. [De Mestre, cap. I, pp. 17-8]), que se valem de conceitos de cálculo diferencial, que ainda não foram abordados aqui, porém.
(9) A rigor, por causa dessa razão entre dois comprimentos, essa medida angular deveria ser adimensional. De fato, muitas vez a unidade "radianos" (rad) é omitida na literatura. voltar
(10) Cf. [Yoshiwara], cap VI, [MacTutor], letra R, e [Chemeurope], verbete Radian. voltar
(11) São as séries Taylor-MacLaurin para as funções trigonométricas aprendidas por estudantes de Cálculo I, cuja forma geral para uma função f(x) é:
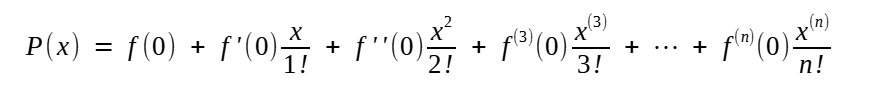
Em que f(n)(0) é enésima derivada de f(x) no ponto zero (cf. futuro capítulo sobre cálculo). Dada a natureza cíclica das funções sen (x) e cos (x) - ambas com período 2π - e o fato de conseguirmos todos os seus valores no intervalo [0, 2π] a partir dos resultados no intervalo [0, π/2] (ex: cos (x) = cos (2π -x) ou sen(x) = - sen (π + x)), então podemos utilizar as séries de seno e cosseno para o valor de qualquer função trigonométrica com a precisão desejada.
As séries podem ser utilizadas para ângulo em graus ou qualquer outra unidade contanto que se faça a conversão para radianos, por meio de uma "regra de três", antes de aplicá-las. Sua dedução, por outro lado, dependeu do uso da métrica por arcos. Por exemplo, o limite
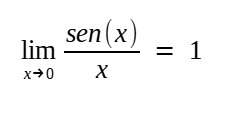
é um passo necessário para o cálculo da funções derivadas de sen (x) e cos (x), porém sua determinação só é possível se valendo (mesmo que indiretamente) do conceito de radianos. voltar
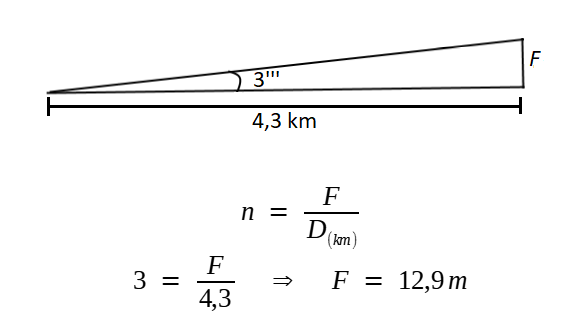
(12) A definição original de Charles-Marc Dapples, um millième é o ângulo sob o qual vemos um metro à distância de 1.000m, ou o ângulo cuja tangente é aproximada 0,001. voltar
(13) Como as funções atan() de C ou math.atan() de Python. Ambas recebem como parâmetro um valor em radianos. voltar
(14) "Chart direction", no original, que é definido como (FT 155-AR, introdução, p. LXVIII): "o lançamento da direção do vento (acrescido de 6400 quando necessário) menos o lançamento da direção de tiro". Uma definição similar pode ser encontrado no manual C6-40 (2001), vol. II, p. 16-12. voltar
(15) Como curiosidade, para cada linha da tabela C exemplificada, Wz2 + Wx2 ≈ 1, como haveríamos de esperar na relação sen2θ + cos2θ = 1. voltar
(16) [McCoy], cap. III, p.43, informa que, para trajetórias tensas de armas de pequeno cablibre, o erro pode ser menor que 1%. voltar
- Calçada, Caio Sérgio & Sampaio, José Luiz; Física Clássica - Cinemática, 1994.
- ChemEurope Encyclopedia, acessado em 16/12/2023.
- Dapples, Charle-Marc; Le millième des artilleurs, publica em Bulletin Techninique de la Suisse Romande, 1915.
- De Mestre, Neville; The Mathematics of Projectiles in Sport, Cambridge Universtiy Press, 1991.
- Dugas, René; A History of Mechanics, tradução inglesa de M.R. Maddox, Routledge & Kegan Paul LTD., Inglaterra, 1957.
- Galilei, Galileu; Dialogue of Two New Sciences, tradução inglesa de Henry Crew e Alfonso de Salvio, MacMillan Company, 1914.
- Hawking, Stephen; Os Gênios da Ciência - sobre os Ombros de Gigantes, Campus, 2005 [contém traduções em português de obras de Copérnico, Galileu, Kepler, Newton e Einstein, prefaciadas por Hawking].
- Litz, Bryan; Applied Ballistics for Long-Range, Applied Ballistics, 3ª ed., 2015.
- McCoy, Robert; Modern Exterior Ballistics, Schiffer Publishing, 2ª ed., 2012.
________; Aerodynamic Drag Modeling for Ballistics, ,1em/11/2023.
- MacTutor, acessado em 16/12/2023.
- Yoshiwara, Katherine; Trigonometry, acessado em 16/12/2023.